The question is incomplete! Complete question along with answer and step by step explanation is provided below.
Question:
Which point on the y-axis lies on the line that passes through point C and is perpendicular to line AB?
A. (-6, 0)
B. (0, -6)
C. (0, 2)
D. (2, 0)
The graph of the question is attached.
Answer:
The point is (x, y) = (0, 2)
The correct option is C.
Therefore, the point (0, 2) on the y-axis lies on the line that passes through point C and is perpendicular to line AB.
Explanation:
From the given graph, the points A and B are
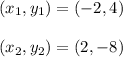
The slope of the equation is given by
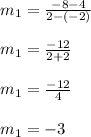
We know that the slopes of two perpendicular lines are negative reciprocals of each other.
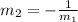
So the slope of the other line is
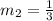
Now we can find the equation of the line that is perpendicular to the line AB and passes through the point C.
From the graph, the coordinates of point C are

The point-slope form is given by,

Substitute the value of slope and the coordinates of point C
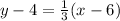
To get the y-intercept, substitute x = 0
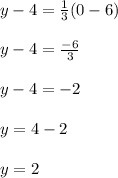
So, the point is
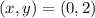
The correct option is C.
Therefore, the point (0, 2) on the y-axis lies on the line that passes through point C and is perpendicular to line AB.