Question

The sand used for sanding icy roads in the winter is stored in a conical-shaped structure with a radius of 10 m and a height of 16 m. Calculate the maximum amount of sand which can be stored in this structure.

Answer 1

1675.52 cubic meters.

Explanation:

First, we establish that the maximum amount of sand that can be stored in the structure is the volume of the conical structure.

`\text{Volume of a Cone }= (1)/(3)\pi r^2 h$ where: \left\{\begin{array}{ll}$r=Base radius\\$h=height of the cone\\-----\\r=10m\\h=16m\end{array}\right`

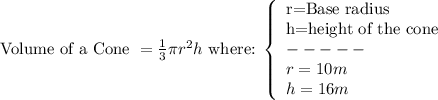
Therefore:

`\text{Volume of the structure}= (1)/(3)\pi * 10^2 * 16\\=(1600\pi)/(3) $ cubic meters\\\approx 1675.52$ m^3 $(correct to 2 d.p)`

The maximum amount of sand that can be stored in the structure is 1675.52 cubic meters.