Letry. 14 Chapter 9: Chapter 9 rest Chapter Test A roof has a cross section that is a right triangle. The diagram shows the approximate dimensions of this cross section. Find th…

Question

asked Sep 21, 2021 98.2k views

2 Answers

Chmoelders · Answer 1 · 2021-09-25T02:59:01+0000

Answer:

h = 7.1 cm

Explanation:

To find the height of the triangle, we can first find the area of the triangle using the Heron's formula:

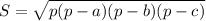
S = √(p(p-a)(p-b)(p-c))

Where a, b and c are the sides of the triangle and p is the semi perimeter of the triangle:

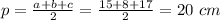
$p = (a+b+c)/(2) = (15 + 8 + 17 )/(2) = 20\ cm$

So the area of the triangle is:

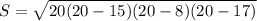
S = √(20(20-15)(20-8)(20-17))

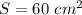
$S = 60\ cm^2$

Now, to find the height, we can use the following equation for the area of the triangle:

S = base * height/2

The height draw in the figure is relative to the side of 17 cm, so this side is the value of base used in the formula. So we have that:

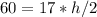
60 = 17 * h/2

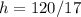
h = 120/17

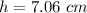
$h = 7.06\ cm$

Rounding to the nearest tenth, we have h = 7.1 cm