Question

PLEASE HELP!! laboratory tests show that the lives of light bulbs are normally distributed with a mean of 750 hours and a standard deviation of 75 hours. find the probability that a randomly selected light bulb will last between 900 and 975 hours.

Answer 1

2.35 babyyyyyyyyyyy

Explanation:

Acellus sux

Answer 2

P = 0.0215 = 2.15%

Explanation:

First we need to convert the values of 900 and 975 to standard scores using the equation:

`z = (x - \mu)/(\sigma)`

Where z is the standard value, x is the original value,
`\mu` is the mean and
`\sigma` is the standard deviation. So we have that:

standard value of 900:
`z = (900 - 750)/(75) = 2`

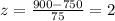
standard value of 975:
`z = (975 - 750)/(75) = 3`

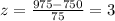
Now, we just need to look at the standard distribution table (z-table) for the values of z = 2 and z = 3:

z = 2 -> p_2 = 0.9772

z = 3 -> p_3 = 0.9987

We want the interval between 900 and 975 hours, so we need the interval between z = 2 and z = 3, so we just need to subtract their p-values:

P = p_3 - p_2 = 0.9987 - 0.9772 = 0.0215

So the probability is 0.0215 = 2.15%