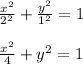Find the equation of the following ellipse based on the following information: Vertices: (-2,0), (2,0) minor axis of length 2

Question

asked Oct 26, 2021 193k views

1 Answer

Egor Klepikov · Answer 1 · 2021-10-30T01:50:56+0000

Answer:

The expression of the ellipse is:
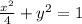
(x^2)/(4) + y^2 = 1

Explanation:

The equation of a ellipse can be written by the following expression:

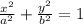
(x^2)/(a^2) + (y^2)/(b^2) = 1

Where 2a is the length of the major axis and 2b is the length of the minor axi. Since we were given the length of the minor vertex, then:

$2b = 2\\b = 1$

The length of the major axis is the distance between the two vertices.

$2a = √([2 - (-2)]^2)\\2a = √((2 + 2)^2)\\2a = √(4^2)\\2a = 4\\a = 2$

Therefore the expression of the ellipse is:

$(x^2)/(2^2) + (y^2)/(1^2) = 1\\\\(x^2)/(4) + y^2 = 1$