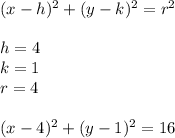Answer:
Circle B:
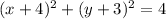
Circle F:
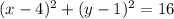
Explanation:
We can write the equation of a circle equation with center on (h,k) and radius r as:

Then, we analyze the circle will have for the circle B:
- It has a center in x=-4 and y=-3.
- It radius can be calculated from the distance from the center (x,y)=(-4,-3) to one of its points (x,y)=(-4, -1). Then, its radius is r=2.
Then, we can write the equation as:
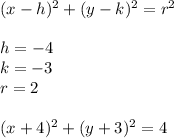
we analyze the circle will have for the circle F:
- It has a center in x=4 and y=1.
- It radius can be calculated from the distance from the center (x,y)=(4, 1) to one of its points (x,y)=(0, 1). Then, its radius is r=4.
Then, we can write the equation as: