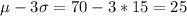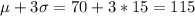Question

COF

A normal distribution curve, where x = 70 and o = 15,
was created by a teacher using her students' grades.
What information about their performances can be
obtained by analyzing the curve?

Answer 1

`X \sim N(\mu= 70, \sigma=15)`

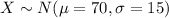
From this info and using the empirical rule we know that we will have about 68% of the scores between:

`\mu -\sigma = 70-15=55`

`\mu +\sigma = 70+15=85`

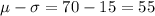
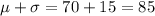
95 % of the scores between:

`\mu -2\sigma = 70-2*15=40`

`\mu +2\sigma = 70+2*15=100`

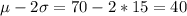
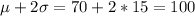
And 99.7% of the values between

`\mu -3\sigma = 70-3*15=25`

`\mu +3\sigma = 70+3*15=115`

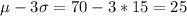
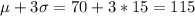
Explanation:

For this problem we can define the random variable of interest as "the student grades" and we know that the distribution for X is given by:

`X \sim N(\mu= 70, \sigma=15)`

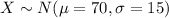
From this info and using the empirical rule we know that we will have about 68% of the scores between:

`\mu -\sigma = 70-15=55`

`\mu +\sigma = 70+15=85`

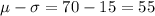
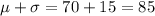
95 % of the scores between:

`\mu -2\sigma = 70-2*15=40`

`\mu +2\sigma = 70+2*15=100`

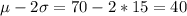
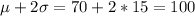
And 99.7% of the values between

`\mu -3\sigma = 70-3*15=25`

`\mu +3\sigma = 70+3*15=115`