Question

What is the quotient of (2x^4-3x^3–3x^2+7x-3)/(c^2-2x+1)

Answer 1

`2x^2 + x - 3`

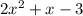
Explanation:

We want to divide
`2x^4 - 3x^3 - 3x^2 + 7x - 3` by
`x^2 - 2x + 1`

To do the long division, divide each term by
`x^2` and then subtract the product of the result and
`x^2 - 2x + 1` from the remaining part of the equation.

Whatever term/value you obtain from each step of the division is a part of the quotient.

When you reach 0, you have gotten to the end of the division.

Check the steps carefully and follow them below:

Step 1:

Divide
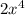`2x^4` by
`x^2`. You get
`2x^2`.

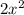Step 2

Multiply
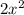`2x^2` by
`x^2 - 2x + 1` and subtract from
`2x^4 - 3x^3 - 3x^2 + 7x - 3`:

`2x^4 - 3x^3 - 3x^2 + 7x - 3 - (2x^4 - 4x^3 + 2x^2)` =
`x^3 - 5x^2 + 7x - 3`

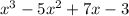
Step 3

Divide
`x^3` by
`x^2`. You get x.

Step 4

Multiply x by
`x^2 - 2x + 1` and subtract from
`x^3 - 5x^2 + 7x - 3`:

`x^3 - 5x^2 + 7x - 3 - (x^3 - 2x^2 + x) = -3x^2 +6x - 3`

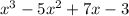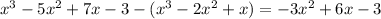
Step 5

Divide
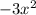`-3x^2` by
`x^2`. You get -3

Step 6

Multiply -3 by
`x^2 - 2x + 1` and subtract from
`-3x^2 +6x - 3`:

`-3x^2 +6x - 3 - (-3x^2 + 6x -3) = 0`

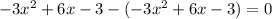
From the three divisions, we got
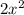`2x^2`, x and -3.

Therefore, the quotient is
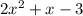`2x^2 + x - 3`.