Question

Write a set of data that contains 12 values for which the box plot has no whiskers. State the median, first and third quartiles, and lower and upper extreme

Answer 1

The data set is:

S = {4.5, 4.5, 4.5, 4.5, 6, 8, 10, 12, 13.5, 13.5, 13.5, 13.5}

Explanation:

Consider the ordered data set:

S = {4.5, 4.5, 4.5, 4.5, 6, 8, 10, 12, 13.5, 13.5, 13.5, 13.5}

The lower extreme is: 4.5

The upper extreme is: 13.5

The median for an even number of observations is the mean of the middle two values.

`\text{Median}=(6^(th)+7^(th))/(2)=(8+10)/(2)=9`

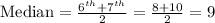
The first quartile (Q₁) is defined as the mid-value between the minimum figure and the median of the data set.

Q₁ = 4.5

The 3rd quartile (Q₃) is the mid-value between the median and the maximum figure of the data set.

Q₃ = 13.5

A box plot that has no whiskers has, Range = Interquartile Range.

Compute the range as follows:

`Rangw=Max.-Min.=13.5-4.5=9`

Compute the Interquartile Range as follows:

`IQR=Q_(3)-Q_(1)=13.5-4.5=9`

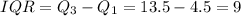
Thus, the box pot for the provided data has no whiskers.