Answer:
The data set is:
S = {4.5, 4.5, 4.5, 4.5, 6, 8, 10, 12, 13.5, 13.5, 13.5, 13.5}
Explanation:
Consider the ordered data set:
S = {4.5, 4.5, 4.5, 4.5, 6, 8, 10, 12, 13.5, 13.5, 13.5, 13.5}
The lower extreme is: 4.5
The upper extreme is: 13.5
The median for an even number of observations is the mean of the middle two values.
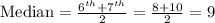
The first quartile (Q₁) is defined as the mid-value between the minimum figure and the median of the data set.
Q₁ = 4.5
The 3rd quartile (Q₃) is the mid-value between the median and the maximum figure of the data set.
Q₃ = 13.5
A box plot that has no whiskers has, Range = Interquartile Range.
Compute the range as follows:
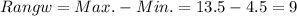
Compute the Interquartile Range as follows:
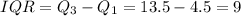
Thus, the box pot for the provided data has no whiskers.