Question

Does the problem involve permutations or​ combinations? Do not solve. From 8 names on a​ ballot, a committee of 5 will be elected to attend a political national convention. How many different committees are​ possible?

Answer 1

Answer: Combination

There are 56 committees possible

============================================

Step-by-step explanation:

The reason why we know we'll use a combination (instead of a permutation) is because order does not matter. There are no ranking positions on a committee. No one person has a special job compared to the other. The ordering of a committee doesn't matter. All that matters is the entire group itself. For instance, if we had people A,B,C then the committee ABC is the same as CBA and BAC. We would have to introduce a different person, say person D, to get a new committee group.

We have n = 8 people overall to choose from and r = 5 slots to fill. Use the combination formula to get

`_n C _r = (n!)/(r!*(n-r)!)\\\\_8 C _5 = (8!)/(5!*(8-5)!)\\\\_8 C _5 = (8!)/(5!*3!)\\\\_8 C _5 = (8*7*6*5!)/(5!*3!)\\\\_8 C _5 = (8*7*6)/(3!)\\\\_8 C _5 = (8*7*6)/(3*2*1)\\\\_8 C _5 = (56*6)/(6)\\\\_8 C _5 = 56\\\\`

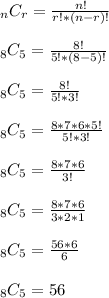
We can conclude there are 56 different committees possible.