Question

the mean monthly income of trainees at a local mill is 1100 with a standard deviation of 150. find rthe probability that a trainee earns less than 900 a month g

Answer 1

The probability is
`P(X < 900 ) = 0.0918`

Explanation:

From the question we are told that

The sample mean is
`\= x = 1100`

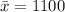
The standard deviation is
`\sigma = 150`

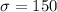
The random number value is x =900

The probability that a trainee earn less than 900 a month is mathematically represented as

`P(X < x) = P((X -\= x)/(\sigma) < (x -\= x)/(\sigma) )`

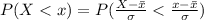
Generally the z-value for the normal distribution is mathematically represented as

`z = (x -\mu )/(\sigma )`

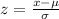
So From above we have

`P(X < 900 ) = P(Z < (900 -1100)/(150) )`

`P(X < 900 ) = P( Z <-1.33)`

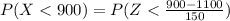
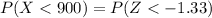
Now from the z-table

`P(X < 900 ) = 0.0918`