Question

The SAT scores have an average of 1200 with a standard deviation of 60. A sample of 36 scores is selected. a) What is the probability that the sample mean will be larger than 1224

Answer 1

the probability that the sample mean will be larger than 1224 is 0.0082

Explanation:

Given that:

The SAT scores have an average of 1200

with a standard deviation of 60

also; a sample of 36 scores is selected

The objective is to determine the probability that the sample mean will be larger than 1224

Assuming X to be the random variable that represents the SAT score of each student.

This implies that ;

`S \sim N ( 1200,60)`

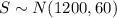
the probability that the sample mean will be larger than 1224 will now be:

`P(\overline X > 1224) = P((\overline X - \mu )/((\sigma)/(√(n)) )> \frac{}{}(1224- \mu )/((\sigma)/(√(n)) ))`

`P(\overline X > 1224) = P(Z > (1224- 1200 )/((60)/(√(36)) ))`

`P(\overline X > 1224) = P(Z > (24 )/((60)/(6) ))`

`P(\overline X > 1224) = P(Z > (24 )/(10) })`

`P(\overline X > 1224) = P(Z > 2.4 })`

`P(\overline X > 1224) =1 - P(Z \leq 2.4 })`

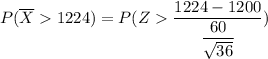
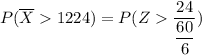
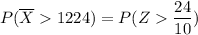
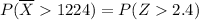
From Excel Table ; Using the formula (=NORMDIST(2.4))

P(\overline X > 1224) = 1 - 0.9918

P(\overline X > 1224) = 0.0082

Hence; the probability that the sample mean will be larger than 1224 is 0.0082