Question

The graph of an absolute value function has a vertex of (2,3) and crosses the x-axis at (−1,0) and (5,0). What is the equation for this absolute value function when y=0? A 0=|x+2|+3 B 0=|x−2|+3 C 0=−|x+2|+3 D 0=−|x−2|+3

Answer 1

I got this question on my test and I answered D cause if you look up the graph it matches the question

Explanation:

D 0=−|x−2|+3

Answer 2

Option D.

Explanation:

The vertex form of an absolute function is

`y=a|x-h|+k`

where, a is a constant, (h,k) is vertex.

It is given that, vertex of an absolute function is (2,3). So, h=2 and k=3.

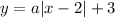`y=a|x-2|+3` ...(1)

It crosses the x-axis at (5,0). So put x=5 and y=0 to find the value of a.

`0=a|5-2|+3`

`-3=3a`

`-1=a`

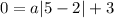
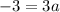
Put a=-1 in (1).

`y=(-1)|x-2|+3`

`y=-|x-2|+3`

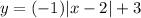
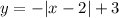
Now, put y=0, to find the equation for this absolute value function when y=0.

`0=-|x-2|+3`

Therefore, the correct option is D.