Question

An object is dropped from the top of a tower with a height of 1160 feet. Neglecting air resistance, the height of the object at time t seconds is given by the

polynomial - 16t square + 1160. Find the height of the object at t = 1 second.
The height of the object at 1 second is feet.

Answer 1

Height at t = 1 sec is 1144 ft

Explanation:

Given:

Initial height of object = 1160 feet

Height of object after t seconds is given by the polynomial:

`- 16t ^2+ 1160`

Let
`h(t)=- 16t ^2+ 1160`

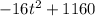
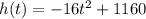
Let us analyze the given equation once.

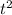`t^2` will always be positive.

and coefficient of
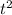`t^2` is
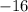`-16` i.e. negative value.

It means something is subtracted from 1160 ft (i.e. the initial height).

So, height will keep on decreasing with increasing value of t.

Also, given that the object is dropped from the top of a tower.

To find:

Height of object at t = 1 sec.

OR

`h (1)` = ?

Solution:

Let us put t = 1 in the given equation:
`h(t)=- 16t ^2+ 1160`

`h(1)=- 16* 1 ^2+ 1160\\\Rightarrow h(1) = -16 + 1160\\\Rightarrow h(1) = 1144\ ft`

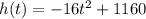
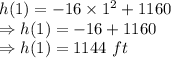
So, height of object at t = 1 sec is 1144 ft.