Question

a box of tickets has an average of 100, and an SD of 20. Four hundred draws will be made at random with replacement from this box. a) Estimate the chance that the average of the draws will be in the range 80 to 120. b) estimate the chance that the average of the draws will be in the range 99 to 101

Answer 1

(a) The probability that the average of the draws will be in the range 80 to 120 is 1.

(b) The probability that the average of the draws will be in the range 99 to 101 is 0.6827.

Explanation:

According to the Central Limit Theorem if we have an unknown population with mean μ and standard deviation σ and appropriately huge random samples (n > 30) are selected from the population with replacement, then the distribution of the sample mean will be approximately normally distributed.

Then, the mean of the sample means is given by,

`\mu_(\bar x)=\mu`

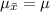
And the standard deviation of the sample means is given by,

`\sigma_(\bar x)=(\sigma)/(√(n))`

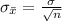
As the sample selected is quite large, i.e. n = 400 > 30, then the sampling distribution of sample means will be approximately normally distributed.

Compute the mean and standard deviation of sample mean as follows:

`\mu_(\bar x)=\mu=100\\\\\sigma_(\bar x)=(\sigma)/(√(n))=(20)/(√(400))=1`

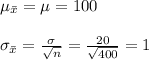
So,
`\bar X\sim N(100, 1)`

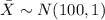
(a)

Compute the probability that the average of the draws will be in the range 80 to 120 as follows:

`P(80<\bar X<120)=P((80-100)/(1)<(\bar X-\mu_(\bar x))/(\sigma_(\bar x))<(120-100)/(1))`

`=P(-20<Z<20)\\\\=P(Z<20)-P(Z<-20)\\\\=(\approx1)-(\approx0)\\\\=1`

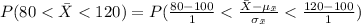
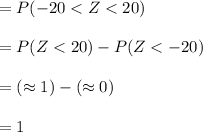
Thus, the probability that the average of the draws will be in the range 80 to 120 is 1.

(b)

Compute the probability that the average of the draws will be in the range 99 to 101 as follows:

`P(99<\bar X<101)=P((99-100)/(1)<(\bar X-\mu_(\bar x))/(\sigma_(\bar x))<(101-100)/(1))`

`=P(-1<Z<1)\\\\=P(Z<1)-P(Z<-1)\\\\=0.6827`

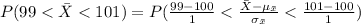
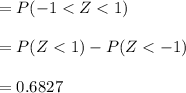
Thus, the probability that the average of the draws will be in the range 99 to 101 is 0.6827.