Question

what is the sum of the values of x that are solutions to the equation x^2 - 10x - 22 = 2 ? a. -12 b. -10 c. -2 d. 2 e. 10

Answer 1

12 and 2

Explanation:

factor the euqation x^2-10x-22=2 and you get (x,-12)(x,2)=0 and when you solve that you get 12 and 2

Answer 2

`x = 2, 12`

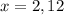
Your correct answer is D, since I don't see a -12.

Step 1: Subtracting 2 from both sides

Since we have to find the value of x, we have to factor the equation. To do so, we first have to subtract the two from both sides of the equation so all the values are on one side of the equation.

`x^2-10x-22(-2)=2(-2)\\x^2-10x-24=0`

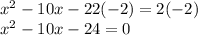
Step 2: Factoring the equation

Part 1

After subtracting 2 from both sides of the equation, we have to factor the polynomial to be able to get it into two sets of parentheses, so in order to do that, we will ignore the equal sign and the 0 for now. We are now left with:

`x^2-10x-24\\`

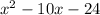
First, we find the multiples of the first term,
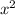`x^2\\`, and the last term, -24. Since there is an invisible 1 before the first term, we are basically finding the multiples of
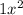`1x^2`, which is
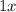`1x` and
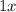`1x`, or x and x. Now we have to find the correct set of numbers for -24. Do do that, we have to make sure that when we multiply the first set of numbers (x, x) with the second set (?, ?) and add them together, then we would get the number in the middle (-10x). So: Two of the most obvious multiples for 24 are 6 and 4, 12 and 2, and 3 and 8. But, this is a negative 24, so we have to work ahead to find out which pair we use first. If we multiply 8 and 3 with x and x, we get 8x and 3x. When we add them together, we do not get 10x, but instead, we get 11x, so it is the wrong pair. If we do the same thing to 6 and 4, we would get 10x, but since 24 is negative, it is not correct because we would need one of the numbers to be negative. In this case, they equal to 10x, but one of the numbers would have to be negative because (if 6 was the negative):

`-6 * 4=-24\\`

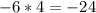
But:

`4-6\\eq 10\\`

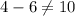
So this is not the correct set either. Our last set is 12 and 2, and when we multiply by x (12x and 2x) and we set one of the numbers to be a negative (-12) and subtract them, we get -10x, so, therefore, this is the correct number pair.

`-12*2=-24\\2-12=-10`

Part 2

With all that done, we now have to factor the numbers. We take the first numbers (x and x), and we place them in front of each of the two parentheses.

`(x,?)(x,?)`

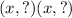
Now, we place -12 and 2 in those places.

`(x,-12)(x,2)`

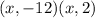
To find x, we have to plug in the equal sign and 0 from the beginning.

`(x,-12)(x,2)=0`

Since they both have to equal to 0, then that means there would be two different answers because, for example: 12 - 12 = 0, but 12 - 2 ≠ 0.

To find both solutions, we treat the numbers in each of the parentheses as its own equation, and we solve it from there.

x - 12 = 0

12 - 12 = 0

x - 2 = 0

2 - 2 = 0

12 and 2 are our solutions! Hope this helps :)