Question

Consider the following scores. (i) a score of 40 from a distribution with mean 50 and standard deviation 10 (ii) a score of 45 from a distribution with mean 50 and standard deviation 5 How do the two scores compare relative to their respective distributions

Answer 1

The scores are equal

Explanation:

The z-score for any normal distribution is:

`z=(X-\mu)/(\sigma)`

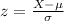
(i) Score (X) = 40

Mean (μ)= 50

Standard deviation (σ) = 10

`z=(40-50)/(10)\\ z=-1`

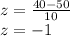
(ii) Score (X) = 45

Mean (μ)= 50

Standard deviation (σ) = 5

`z=(45-50)/(5)\\ z=-1`

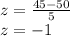
Both scores have the same z-score, which means that, relative to their respective distributions, the scores are equal.