Question

Five thousand tickets are sold at​ $1 each for a charity raffle. Tickets are to be drawn at random and monetary prizes awarded as​ follows: 1 prize of ​$500​, 3 prizes of ​$300​, 5 prizes of ​$50​, and 20 prizes of​ $5. What is the expected value of this raffle if you buy 1​ ticket?

Answer 1

the expected value of this raffle if you buy 1​ ticket = -0.65

Explanation:

Given that :

Five thousand tickets are sold at​ $1 each for a charity raffle

Tickets are to be drawn at random and monetary prizes awarded as​ follows: 1 prize of ​$500​, 3 prizes of ​$300​, 5 prizes of ​$50​, and 20 prizes of​ $5.

Thus; the amount and the corresponding probability can be computed as:

Amount Probability

$500 -$1 = $499 1/5000

$300 -$1 = $299 3/5000

$50 - $1 = $49 5/5000

$5 - $1 = $4 20/5000

-$1 1- 29/5000 = 4971/5000

The expected value of the raffle if 1 ticket is being bought is as follows:

`E(x) = \sum x * P(x)`

`E(x) = (499 * (1)/(5000) + 299 *(3)/(5000) + 49 *(5)/(5000) + 4 * (20)/(5000) + (-1 * (4971)/(5000) ))`

`E(x) = (0.0998 + 0.1794+0.049 + 0.016 + (-0.9942 ))`

`E(x) = (0.3442 -0.9942 )`

`\mathbf{E(x) = -0.65}`

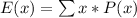
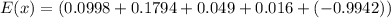
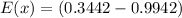
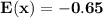
Thus; the expected value of this raffle if you buy 1​ ticket = -0.65