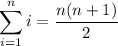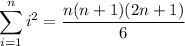Question

Find the approximate area between the curve f(x) = -4x² + 32x and on the x-axis on the interval [0,8] using 4 rectangles. Use the right endpoint of each rectangle to determine the height.

Answer 1

320 square units

Explanation:

Answer 2

Split up the interval [0, 8] into 4 equally spaced subintervals:

[0, 2], [2, 4], [4, 6], [6, 8]

Take the right endpoints, which form the arithmetic sequence

`r_i=2+\frac{8-0}4(i-1)=2i`

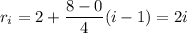
where 1 ≤ i ≤ 4.

Find the values of the function at these endpoints:

`f(r_i)=-4{r_i}^2+32r_i=-16i^2+64i`

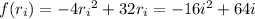
The area is given approximately by the Riemann sum,

`\displaystyle\int_0^8f(x)\,\mathrm dx\approx\sum_(i=1)^4f(r_i)\Delta x_i`

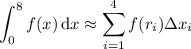
where
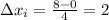`\Delta x_i=\frac{8-0}4=2`; so the area is approximately

`\displaystyle2\sum_(i=1)^4(-16i^2+64i)=-32\sum_(i=1)^4i^2+128\sum_(i=1)^4i=-32\cdot\frac{4\cdot5\cdot9}6+128\cdot\frac{4\cdot5}2=\boxed{320}`

where we use the formulas,

`\displaystyle\sum_(i=1)^ni=\frac{n(n+1)}2`

`\displaystyle\sum_(i=1)^ni^2=\frac{n(n+1)(2n+1)}6`