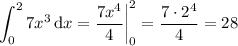Split up the interval [0, 2] into n equally spaced subintervals:
![\left[0,\frac2n\right],\left[\frac2n,\frac4n\right],\left[\frac4n,\frac6n\right],\ldots,\left[\frac{2(n-1)}n,2\right]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/oy3zvxd7mcs7r5l00sx5m2saib35xmeygo.png)
Let's use the right endpoints as our sampling points; they are given by the arithmetic sequence,
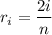
where
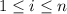 . Each interval has length
. Each interval has length
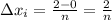 .
.
At these sampling points, the function takes on values of
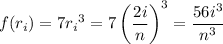
We approximate the integral with the Riemann sum:
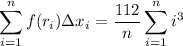
Recall that
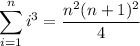
so that the sum reduces to
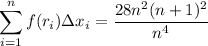
Take the limit as n approaches infinity, and the Riemann sum converges to the value of the integral:
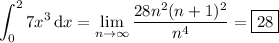
Just to check: