Answer:
The correct option is (B).
Explanation:
The median (m) is a measure of central tendency. To obtain the median, we assemble the data in arising order. If the data is odd, the median is the mid-value. If the data is even, the median is the arithmetic-mean of the two mid-values.
The mean of a data set is:
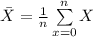
For the three kittens it is provided that the weights are in the range 147 g to 159 g.
So, the mean and median weight for the 3 kittens lies in the middle of this range.
Now a fourth kitten is born, with weight 57 g.
Now the range of the weight of 4 kittens is, 57 g to 159 g.
The mean is going to decrease as one more value is added to the data and the value is the least.
The median will also decrease because now the median will be mean of the 2nd and 3rd values.
But the mean would decrease more than the median because a smaller value is added to the data.
Thus, the correct option is (B).