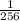Answer:
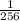
Explanation:
Geometric sequence means there is a common ratio. All that means is term divided previous term is the same across your sequence.
ONE WAY:
So we are given here that:
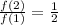 and that the first term which is
and that the first term which is
 is 2.
is 2.
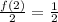
This implies
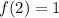 after multiplying both sides by 2 and getting that
after multiplying both sides by 2 and getting that
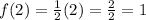 .
.
So you have that
2,1,...
basically you can just multiply by 1/2 to keep generating more terms of the sequence.
Third term would be
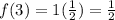 .
.
Fourth term would be
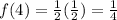 .
.
...keep doing this til you get to the 10th term.
ANOTHER WAY:
Let's make a formula.
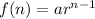
 is the first term.
is the first term.
 is the common ratio.
is the common ratio.
And we want to figure out what happens at
 .
.
Let's plug in our information we have
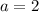
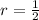 :
:
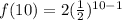
Put into calculator or do by hand...
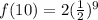
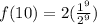
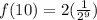

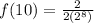
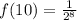
Scratch work:
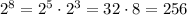 .
.
End scratch work.
The answer is that the tenth term is