Answer:
the guarantee period should be less than 136010 miles
Explanation:
From the given information;
Let consider Y to be the life of a car engine
with a mean μ = 170000
and a standard deviation σ = 16500
The objective is to determine what should be the guarantee period T if the company wants less than 2% of the engines to fail.
i.e
P(Y < T ) < 0.02
For the variable of z ; we have:
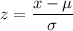
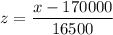
Now;

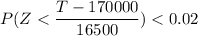
From Z table ;
At P(Z < -2.06) ≅ 0.0197 which is close to 0.02
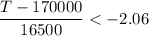
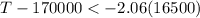


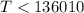
Thus; the guarantee period should be less than 136010 miles