Answer:
Approximately
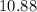 .
.
Step-by-step explanation:
Equilibrium constant
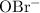 can act as a weak Bronsted-Lowry base:
can act as a weak Bronsted-Lowry base:
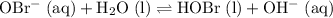 .
.
(Side note: the state symbol of
 in this equation is
in this equation is
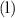 (meaning liquid) because
(meaning liquid) because
 is a weak acid.)
is a weak acid.)
However, the equilibrium constant of this reaction,
 , isn't directly given. The idea is to find
, isn't directly given. The idea is to find
 using the
using the
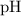 value at the half-equivalence point. Keep in mind that this system is at equilibrium all the time during the titration. If temperature stays the same, then the same
value at the half-equivalence point. Keep in mind that this system is at equilibrium all the time during the titration. If temperature stays the same, then the same
 value could also be used to find the
value could also be used to find the
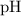 of the solution before the acid was added.
of the solution before the acid was added.
At equilibrium:
![\displaystyle K_\text{eq} = ([\rm HOBr\; (l)]\cdot [\rm OH^(-)\; (aq)])/([\rm OBr^(-)\; (aq)])](https://img.qammunity.org/2021/formulas/chemistry/college/3umc7yj510n4bs50lhyxzunowg60mzoo3y.png) .
.
At the half-equivalence point of this titration, exactly half of the base,
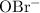 , has been converted to its conjugate acid,
, has been converted to its conjugate acid,
 . Therefore, the half-equivalence concentration of
. Therefore, the half-equivalence concentration of
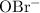 and
and
 should both be equal to one-half the initial concentration of
should both be equal to one-half the initial concentration of
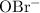 .
.
As a result, the half-equivalence concentration of
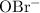 and
and
 should be the same. The expression for
should be the same. The expression for
 can thus be simplified:
can thus be simplified:
![\begin{aligned}& K_\text{eq} \\&= \frac{\left(\text{half-equivalence $[\rm HOBr\; (l)]$}\right)\cdot \left(\text{half-equivalence $[\rm OH^(-)\; (aq)]$}\right)}{\text{half-equivalence $[\rm OBr^(-)\; (l)]$}}\\ &=\text{half-equivalence $[\rm OH^(-)\; (aq)]$}\end{aligned}](https://img.qammunity.org/2021/formulas/chemistry/college/49qnozw0pkhg39lkmjg3omrzmf8zfs3t39.png) .
.
In other words, the
 of this system is equal to the
of this system is equal to the
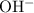 concentration at the half-equivalence point. Assume that
concentration at the half-equivalence point. Assume that
 the self-ionization constant of water, is
the self-ionization constant of water, is
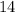 . The concentration of
. The concentration of
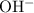 can be found from the
can be found from the
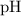 value:
value:
![\begin{aligned}& \text{half-equivalence $[\rm OH^(-)\; (aq)]$} \\ &= 10^{\rm pH - p\mathnormal{K}_\text{w}}\;\rm mol \cdot L^(-1) \\ &= 10^(7.75 - 14)\; \rm mol \cdot L^(-1)\\ &= 10^(-6.25)\; \rm mol \cdot L^(-1)\end{aligned}](https://img.qammunity.org/2021/formulas/chemistry/college/hcupxl6o7swuvpxmgtdshc0x9zvsh74tqp.png) .
.
Therefore,
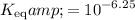 .
.
Initial pH of the solution
Again, since
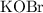 is a soluble salt, all that
is a soluble salt, all that
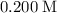 of
of
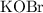 in this solution will be in the form of
in this solution will be in the form of
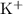 and
and
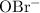 ions. Before any hydrolysis takes place, the concentration of
ions. Before any hydrolysis takes place, the concentration of
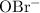 should be equal to that of
should be equal to that of
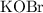 . Therefore:
. Therefore:
![\text{$[\rm OBr^(-)\; (aq)]$ before hydrolysis} = 0.200\; \rm M](https://img.qammunity.org/2021/formulas/chemistry/college/352g3ahhwudosvx3mxkezbi7a03ktp04a5.png) .
.
Let the equilibrium concentration of
![[\rm OH^(-)\; (aq)]](https://img.qammunity.org/2021/formulas/chemistry/college/p0i9gn8qp4upzcim2okj01564zhb38p8m1.png) be
be
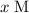 . Create a RICE table for this reversible reaction:
. Create a RICE table for this reversible reaction:
![\begin{array}ccccccc & \rm OBr^(-)\; (aq) &+&\rm H_2O\; (l)& \rightleftharpoons & \rm HOBr\; (l)& + & \rm OH^(-)\; (aq) \\ \textbf{I}& 0.200\; \rm M & & & & 0 \; \rm M & & 0\; \rm M \\ \textbf{C} & -x\; \rm M & & & & +x \; \rm M & & +x\; \rm M \\ \textbf{E}& (0.200 + x)\; \rm M & & & & x \; \rm M & & x\; \rm M \end{array}]() .
.
Assume that external factors (such as temperature) stays the same. The
 found at the half-equivalence point should apply here, as well.
found at the half-equivalence point should apply here, as well.
![\displaystyle K_\text{eq} = ([\rm HOBr\; (l)]\cdot [\rm OH^(-)\; (aq)])/([\rm OBr^(-)\; (aq)])](https://img.qammunity.org/2021/formulas/chemistry/college/3umc7yj510n4bs50lhyxzunowg60mzoo3y.png) .
.
At equilibrium:
![\displaystyle ([\rm HOBr\; (l)]\cdot [\rm OH^(-)\; (aq)])/([\rm OBr^(-)\; (aq)]) = (x^2)/(0.200 + x)](https://img.qammunity.org/2021/formulas/chemistry/college/o3r8tuhsqyub1tw5bvlvwmrfl99tx5anzf.png) .
.
Assume that
 is much smaller than
is much smaller than
 , such that the denominator is approximately the same as
, such that the denominator is approximately the same as
 :
:
![\displaystyle ([\rm HOBr\; (l)]\cdot [\rm OH^(-)\; (aq)])/([\rm OBr^(-)\; (aq)]) = (x^2)/(0.200 + x) \approx (x^2)/(0.200)](https://img.qammunity.org/2021/formulas/chemistry/college/7iv3bjs776v79mxmaf623wz6hqr6jne8z5.png) .
.
That should be equal to the equilibrium constant,
 . In other words:
. In other words:
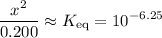 .
.
Solve for
 :
:
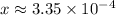 .
.
In other words, the
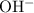 before acid was added was approximately
before acid was added was approximately
 , which is the same as
, which is the same as
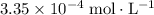 . Again, assume that
. Again, assume that
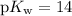 . Calculate the
. Calculate the
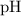 of that solution:
of that solution:
![\begin{aligned}\rm pH &= \rm p\mathnormal{K}_\text{w} + \log [\mathrm{OH^(-)}] \approx 10.88\end{aligned}](https://img.qammunity.org/2021/formulas/chemistry/college/bdsp5b7qb3e20ylehqa4s6zkafxjuoqs24.png) .
.
(Rounded to two decimal places.)