Question

A circle has a radius of 8ft. Find the length s of the arc intercepted by a central angle of π3 radians. Do not round any intermediate computations, and round your answer to the nearest tenth.

Answer 1

8.4ft

Explanation:

Formula for calculating the length of an arc is expressed as
`L = (\theta)/(360) * 2\pi r\\`

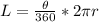
`\theta` is the central angle = π/3 rad

r is the radius of the circle = 8ft

Substituting the values into the formula above we have;

`L =`
`(((\pi)/(3) ))/(2 \pi) * 2\pi (8)\\\\`

`L = (\pi)/(6 \pi) * 2\pi(8) \\\\L = 1/6 * 16\pi\\\\L = 8\pi/3\\\\L = (8(22/7))/(3) \\\\L = (8*22)/(7*3)\\ \\L = 176/21\\\\L = 8.4 ft (to\ the\ nearest\ tenth)`

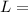
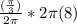
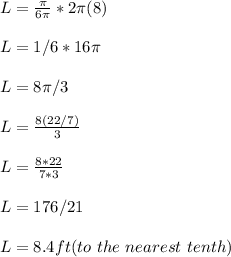
Hence, the length of the arc s is approximately 8.4 ft.