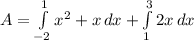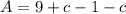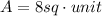Answer:
Explanation:
Complete Question
The complete question is shown on the first uploaded image
Answer:
The area is
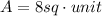
Explanation:
From the question we are told that
The first equation is
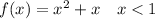
![on[ -2 , 3 ]](https://img.qammunity.org/2021/formulas/mathematics/college/2w040qg9ok4gf4c91gh1g632r3d0peo1bz.png)
The second equation is
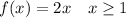
This means that the limit of the area under the enclosed region is limited between -2 to 1 on the x- axis for first equation and 1 to 3 for second equation
Now the area under the region is evaluated as