Question

Consider the matrix A = \begin{pmatrix} 7 & 9 & -3 \\ 3 & -6 & 5 \\ 4 & 0 & 1 \end{pmatrix} ​⎝ ​⎛ ​​ ​7 ​3 ​4 ​​ ​9 ​−6 ​0 ​​ ​−3 ​5 ​1 ​​ ​⎠ ​⎞ ​​ . What is the value of minor M_{11}M ​11 ​​ ? 5 -6 0 -4

Answer 1

The value of M₁₁ is -6.

Explanation:

The minor,
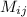`M_(ij)` is the determinant of a square matrix, say P, formed by removing the ith row and jth column from the original square matrix, P.

The matrix provided is as follows:

`A=\left[\begin{array}{ccc}7&9&-3\\3&-6&5\\4&0&1\end{array}\right]`

The matrix M₁₁ is:

Remove the 1st row and 1st column to form M₁₁,

`M_(11)=\left|\begin{array}{cc}-6&5\\4&0\end{array}\right|`

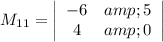
Compute the value of M₁₁ as follows:

`M_(11)=\left|\begin{array}{cc}-6&5\\4&0\end{array}\right|`

`=(-6* 1)-(5* 0)\\\\=-6-0\\=-6`

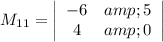
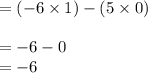
Thus, the value of M₁₁ is -6.