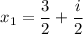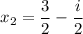Question

What are the solutions of 2x2- 6x+5=0?

Answer 1

`$x_(1)=(3)/(2)+(i)/(2)\\$`

`$x_(2)=(3)/(2)-(i)/(2)$`

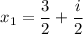
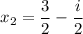
Explanation:

It is a Quadratic Equation

`2x^2-6x+5=0`

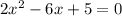
Once it cannot be easily factored, you solve it using the quadratic formula or completing the square. I will use the quadratic formula.

`$x=(-b\pm √(b^2-4ac))/(2a)$`

`$x=(-(-6)\pm√((-6)^2-4\cdot 2\cdot 5))/(2\cdot 2)$`

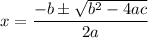
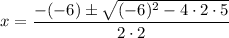
The discriminant is negative, therefore we got complex solutions.

`\Delta= √(-4)= √(4i) =2i`

`$x=(6\pm 2i)/(4)$`

`$x_(1)=(3+i)/(2) $`

`$x_(2)=(3-i)/(2) $`

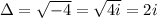
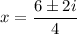
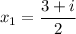
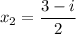
Now, just rewrite the roots in standard complex form

`$x_(1)=(3)/(2)+(i)/(2)\\$`

`$x_(2)=(3)/(2)-(i)/(2)$`