Answer:
Hence, none of the options presented are valid. The plane is represented by
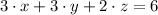 .
.
Explanation:
The general equation in rectangular form for a 3-dimension plane is represented by:
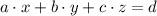
Where:
 ,
,
 ,
,
 - Orthogonal inputs.
- Orthogonal inputs.
 ,
,
 ,
,
 ,
,
 - Plane constants.
- Plane constants.
The plane presented in the figure contains the following three points: (2, 0, 0), (0, 2, 0), (0, 0, 3)
For the determination of the resultant equation, three equations of line in three distinct planes orthogonal to each other. That is, expressions for the xy, yz and xz-planes with the resource of the general equation of the line:
xy-plane (2, 0, 0) and (0, 2, 0)
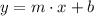
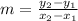
Where:
 - Slope, dimensionless.
- Slope, dimensionless.
 ,
,
 - Initial and final values for the independent variable, dimensionless.
- Initial and final values for the independent variable, dimensionless.
 ,
,
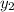 - Initial and final values for the dependent variable, dimensionless.
- Initial and final values for the dependent variable, dimensionless.
 - x-Intercept, dimensionless.
- x-Intercept, dimensionless.
If
 ,
,
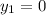 ,
,
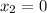 and
and
 , then:
, then:
Slope
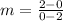
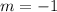
x-Intercept

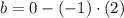
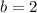
The equation of the line in the xy-plane is
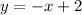 or
or
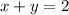 , which is equivalent to
, which is equivalent to
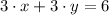 .
.
yz-plane (0, 2, 0) and (0, 0, 3)
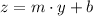
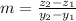
Where:
 - Slope, dimensionless.
- Slope, dimensionless.
 ,
,
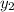 - Initial and final values for the independent variable, dimensionless.
- Initial and final values for the independent variable, dimensionless.
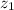 ,
,
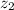 - Initial and final values for the dependent variable, dimensionless.
- Initial and final values for the dependent variable, dimensionless.
 - y-Intercept, dimensionless.
- y-Intercept, dimensionless.
If
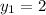 ,
,
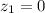 ,
,
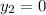 and
and
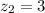 , then:
, then:
Slope
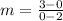
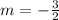
y-Intercept

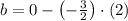

The equation of the line in the yz-plane is
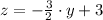 or
or
 .
.
xz-plane (2, 0, 0) and (0, 0, 3)
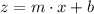
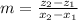
Where:
 - Slope, dimensionless.
- Slope, dimensionless.
 ,
,
 - Initial and final values for the independent variable, dimensionless.
- Initial and final values for the independent variable, dimensionless.
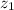 ,
,
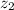 - Initial and final values for the dependent variable, dimensionless.
- Initial and final values for the dependent variable, dimensionless.
 - z-Intercept, dimensionless.
- z-Intercept, dimensionless.
If
 ,
,
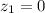 ,
,
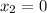 and
and
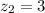 , then:
, then:
Slope
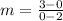
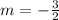
x-Intercept
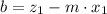
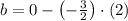

The equation of the line in the xz-plane is
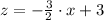 or
or
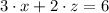
After comparing each equation of the line to the definition of the equation of the plane, the following coefficients are obtained:
 ,
,
 ,
,
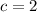 ,
,
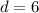
Hence, none of the options presented are valid. The plane is represented by
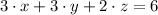 .
.