The answer to the blanks in the prompt are as follows:
- The formula is
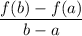
- The value of f(-1) is 2
- The value of f(-4) is 9
- The average rate of change of f(x) over the interval [-4,-1] is
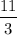
The average rate of change of a function over an interval is the slope of the secant line that intersects the graph of the function at the interval's endpoints.
The formula for the average rate of change of the function f over the interval [a, b] is:
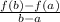
In the case of the graph you sent, the function f is represented by a blue line, and the interval is [4,1]. The y-values of the endpoints of the interval are f(-4)=9 and f(-1)=2.
Therefore, the average rate of change of f over the interval [4,1] is:
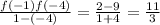 T
T
he average rate of change of the function is
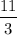 , which means that the function is decreasing at an average rate of
, which means that the function is decreasing at an average rate of
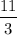 units per unit change in x.
units per unit change in x.