Question

In how many ways can you arrange 4 different colored balls? 4,8,4!,3!,5!

Answer 1

We can arrange 4 different colored balls in 24 ways.

Explanation:

We have to find the number of ways in which we can arrange 4 different colored balls.

Firstly, we have to decide that either we use Permutation or we use Combination.

A Permutation is used when the order of arranging the numbers matters while on the other hand, a combination is used when the order of arranging the numbers doesn't matter.

So, in our question; the ordering matters to us as a ball which is placed in the first place can't be put again put in other places.

Number of ways of arranging 4 different colored balls =
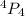
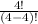`^(4)P_4`

=
`(4!)/((4-4)!)` {
`\because ^(n) P_r = (n!)/((n-r)!)` }

= 4! =
`4 * 3 * 2* 1`

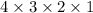
= 24 ways

Hence, we can arrange 4 different colored balls in 24 ways.