Question

I really need help with this

Answer 1

Our system of equations is:

• y+2x+1=0
• 4y-4x²-12x = -7

We are looking for x

Let's express y using x

• y+2x+1=0
• y= -2x-1

Replace x in the second equation with the result

• 4y-4x²-12x = -7
• 4(-2x-1)-4x²-12x = -7
• -8x-4-4x²-12x = -7
• -8x-4x²-12x = -7+4
• -4x²-20x = -3
• -4x²-20x+3 = 0 multiply by -1 to get rid of the - signs with x
• 4x²+20x-3=0

4x²+20x+3=0 is a quadratic equation

Let Δ be our discriminant

• a= 4
• b= 20
• c= -3

Δ= 20²-4*4*(-3)

Δ=448 > 0 so we have two solutions for x

let x and x' be the solutions

• x =
  `(-20-√(448) )/(8)`= -5.145 ≈ -5.15
• x'=
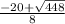  `(-20+√(448) )/(8)`= 0.145≈ 0.15

so the solutions are:

-5.15 and 0.15