Question

Rosalie is organizing a circus performance to raise money for a charity. She is trying to decide how much to charge for tickets. From past experience, she knows that the number of people who will attend is a linear function of the price per ticket. If she charges 5 dollars, 1175 people will attend. If she charges 7 dollars, 935 people will attend. How much should she charge per ticket to make the most money

Answer 1

she should charge $7.395 per ticket in order to make the most money.

Explanation:

From the given information:

If Rosalie charges $5 then 1175 people will attend the circus performance

If Rosalie charges $7 then 935 people will attend the circus performance

Let x be the cost and y to be the number of people that will attend the performance . Then, we will have two points which are;

(5, 1175) and (7, 935)

The slope(m) of this points =
`(\Delta y)/(\Delta x)`

=
`(y_2-y_1)/(x_2-x_1)`

`=(935-1175)/(7-5)`

Slope (m) =
`(-240)/(2)`

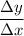
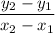
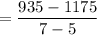
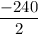
Slope (m) = -120

However; we can now have the linear equation:

`y-y_1 = m(x-x_1)`

`y-1175= -120(x-5)`

`y-1175= -120x+600`

`y= -120x+600+1175`

`y= -120x+1775`

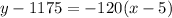
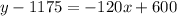
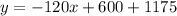
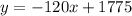
The linear function is : y = -120x + 1775

Now; the total amount of money she can now earn is:

f(x) = xy

f(x) = x(-120x + 1775)

f(x) = -120x² + 1775x

The above expression is a quadratic equation; Using the quadratic formula; we have:

`=(-b \pm √(b^2-4ac))/(2a)`

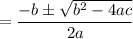
where; a = -120 ; b = +1775 and c = 0

`=(-(1775) \pm √((1775)^2-4(-120)(0)))/(2(-120))`

`=(-(1775) + √((1775)^2-4(-120)(0)))/(2(-120)) \ \ \ \ \ OR \ \ \ \ (-(1775) -√((1775)^2-4(-120)(0)))/(2(-120))`

`=(-(1775) + √((1775)^2))/((-240)) \ \ \ \ \ OR \ \ \ \ (-(1775) -√((1775)^2))/((-240))`

`=(-(1775) + (1775))/((-240)) \ \ \ \ \ OR \ \ \ \ (-(1775) - (1775))/((-240))`

`=(0)/((-240)) \ \ \ \ \ OR \ \ \ \ (-3550)/((-240))`

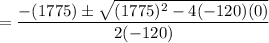
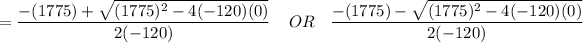
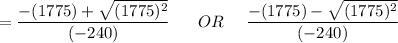
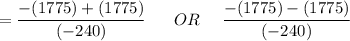
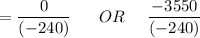
= 0 OR 14.79

Since; we are considering the value greater than zero

x = 14.79

maximum value of x = 14.79/2 = 7.395

Thus ; she should charge $7.395 per ticket in order to make the most money.