Question

Which of the following have the property that a(x)=a−1(x)? I. y=x II. y=1/x III.y=x^2 IV. y=x^3 A. I and II, only B. IV, only C. I, II, and III D. I, only

Answer 1

Correct answer:

A. I and II

Explanation:

First of all, let us have a look at the steps of finding inverse of a function.

1. Replace y with x and x with y.

2. Solve for y.

3. Replace y with
`f^(-1)(x)`

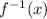
Given that:

`I.\ y=x \\II.\ y=\frac{1}x \\III.\ y=x^2 \\IV.\ y=x^3`

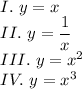
Now, let us find inverse of each option one by one.

I. y = x, a(x) = x

Replacing y with and x with y:

x = y

x =
`a^(-1)(x)` =
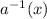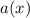`a(x)` Hence, I is true.

II.
`y =(1)/(x)`

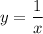
Replacing y with and x with y:

`x =(1)/(y)`

`x=(1)/(a^(-1)(x))`

`\Rightarrow a^(-1)(x) = (1)/(x)`

`a^(-1)(x)` =
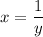
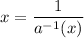
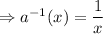
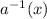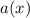`a(x)` Hence, II is true.

III.
`y =x^(2)`

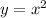
Replacing y with and x with y:

`x =y^(2)\\\Rightarrow y = \sqrt x\\\Rightarrow a^(-1)(x) = √(x) \\e a(x)`

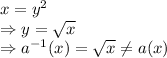
Hence, III is not true.

IV.
`y =x^(3)`

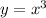
Replacing y with and x with y:

`x =y^(3)\\\Rightarrow y = \sqrt[3] x\\\Rightarrow a^(-1)(x) = \sqrt[3]{x} \\e a(x)`

Hence, IV is not true.

Correct answer:

A. I and II