Question

A multiple-choice test has 30 questions and each one has five possible answers, of which only one is correct. If all answers were guesses, find the probability of getting exactly four correct answers.

Answer 1

Answer: the probability is 0.13

Explanation:

First, each question has 5 options and only one is correct.

Then, selecting at random, the probability of getting a correct answer is equal to:

p = 1/5 = 0.20 (and the probability of getting it incorrect is p = 4/5 = 0.80)

Now, if out of 30 questions, we got 4 correct and 26 incorrect, the probability for a given combination is;

p = (0.20^4)*(0.80^26)

But we also need to multiply this by the total number of combinations.

This is we have 30 questions in total, and we can select 4 of them that will be the correct ones.

Now, if we have N objects in total, the number of different combinations of K elements out of those N elements is

`C = (N!)/((N-K)!*K!)`

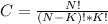
In this case, N = 30 and K = 4.

`C = (30!)/((30 -4)!*4!) = (30*29*28*27)/(4*3*2) = 27,405`

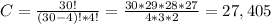
Then the probability of getting exactly 4 correct answers is:

P = (0.20^4)*(0.80^26)*27,405 = 0.13