Question

An article in Fire Technology, 2014 (50.3) studied the effectiveness of sprinklers in fire control by the number of sprinklers that activate correctly. The researchers estimate the probability of a sprinkler to activate correctly to be 0.7. Suppose that you are an inspector hired to write a safety report for a large ballroom with 10 sprinklers. Assume the sprinklers activate correctly or not independently. (a) What is the probability that all of the sprinklers will operate correctly in a fire

Answer 1

probability that all of the sprinklers will operate correctly in a fire: 0.0282

Explanation:

In order to solve this question we will use Binomial probability distribution because:

• In the question it is given that the sprinklers activate correctly or not independently.
• The number of outcomes are two i.e. sprinklers activate correctly or not.

A binomial distribution is a probability of a success or failures outcomes in an repeated multiple or n times.

Number of outcomes of this distributions are two.

The formula is:

b(x; n, P) =
`C_(n,x)*p^(x) * (1 - p)^(n-x)`

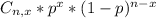
b = binomial probability also represented as P(X=x)

x =no of successes

P = probability of a success on a single trial

n = no of trials

`C_(n,x)` is calculated as:

`C_(n,x)` = n! / x!(n – x)!

= 10! / 10!(10-10)!

= 1

According to given question:

probability of success i.e. p = 0.7 i.e. probability of a sprinkler to activate correctly.

number of trials i.e. n = 10 as number of sprinklers are 10

To find: probability that all of the sprinklers will operate correctly in a fire

X = 10 because we have to find the probability that "all" of the sprinklers will operate correctly and there are 10 sprinklers so all 10 of them

So putting these into the formula:

P(X=x) =
`C_(n,x)*p^(x) * (1 - p)^(n-x)`

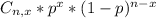
= C₁₀,₁₀ * 0.7¹⁰ * (1-0.7)¹⁰⁻¹⁰

= 1 * 0.0282 * (0.3) ⁰

= 1 * 0.0282 * 1

P(X=x) = 0.0282