Question

This is used for the next few questions: The rating for the new scary movie has a scale of 0 to 10. The average response was that the regular movie attendant enjoyed the movie with 8.3 points and a standard deviation of 0.5 points. What is the percent of people who gave the movie a rating between 6.8 and 8.8? (Write the number as a percent only without a percent sign.)

Answer 1

The percentage that of people who gave the movie a rating between 6.8 and 8.8

P(6.8≤X≤8.8) = 83.9≅ 84 percentage

Explanation:

Step(i):-

Mean of the Population = 8.3 points

Standard deviation of the Population = 0.5 points

Let 'X' be the random variable in normal distribution

Let X = 6.8

`Z = (x-mean)/(S.D) = (6.8-8.3)/(0.5) = -3`

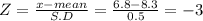
Let X = 8.8

`Z = (x-mean)/(S.D) = (8.8-8.3)/(0.5) = 1`

The probability that of people who gave the movie a rating between 6.8 and 8.8

P(6.8≤X≤8.8) = P(-3≤Z≤1)

= P(Z≤1)- P(Z≤-3)

= 0.5 + A(1) - ( 0.5 -A(-3))

= A(1) + A(3) (∵A(-3)=A(3)

= 0.3413 +0.4986 (∵ From Normal table)

= 0.8399

Conclusion:-

The percentage that of people who gave the movie a rating between 6.8 and 8.8

P(6.8≤X≤8.8) = 83.9≅ 84 percentage