Question

A company rounds its losses to the nearest dollar. The error on each loss is independently and uniformly distributed on [–0.5, 0.5]. If the company rounds 2000 such claims, find the 95th percentile for the sum of the rounding errors.

Answer 1

the 95th percentile for the sum of the rounding errors is 21.236

Explanation:

Let consider X to be the rounding errors

Then;
`X \sim U (a,b)`

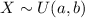
where;

a = -0.5 and b = 0.5

Also;

Since The error on each loss is independently and uniformly distributed

Then;

`\sum X _1 \sim N ( n \mu , n \sigma^2)`

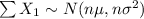
where;

n = 2000

Mean
`\mu = (a+b)/(2)`

`\mu = (-0.5+0.5)/(2)`

`\mu =0`

`\sigma^2 = ((b-a)^2)/(12)`

`\sigma^2 = ((0.5-(-0.5))^2)/(12)`

`\sigma^2 = ((0.5+0.5)^2)/(12)`

`\sigma^2 = ((1.0)^2)/(12)`

`\sigma^2 = (1)/(12)`

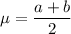
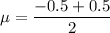
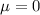
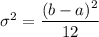
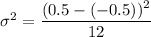
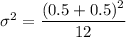
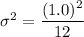
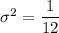
Recall:

`\sum X _1 \sim N ( n \mu , n \sigma^2)`

`n\mu = 2000 * 0 = 0`

`n \sigma^2 = 2000 * (1)/(12) = (2000)/(12)`

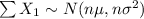
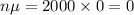
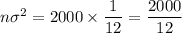
For 95th percentile or below

`P(\overline X < 95}) = P(\frac{\overline X - \mu }{\sqrt{{n \sigma^2}}}< \frac{P_(95)- 0 } {\sqrt{(2000)/(12)}}) =0.95`

`P(Z< \frac{P_(95) } {\sqrt{(2000)/(12)}}) = 0.95`

`P(Z< \frac{P_(95)√(12) } {\sqrt{{2000}}}) = 0.95`

`\frac{P_(95)√(12) } {\sqrt{{2000}}} =1- 0.95`

`\frac{P_(95)√(12) } {\sqrt{{2000}}} = 0.05`

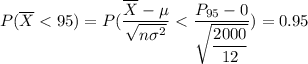
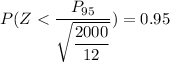
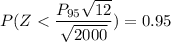
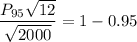
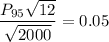
From Normal table; Z > 1.645 = 0.05

`\frac{P_(95)√(12) } {\sqrt{{2000}}} =1.645`

`{P_(95)√(12) } = 1.645 * {\sqrt{{2000}}}`

`{P_(95) = \frac{1.645 * {\sqrt{{2000}}} }{√(12) } }`

`\mathbf{P_(95) = 21.236}`

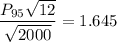
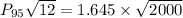
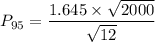
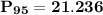
the 95th percentile for the sum of the rounding errors is 21.236