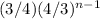Answer:
nth term of geometric sequence = a(n) =
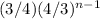
Explanation:
nth term of geometric sequence = a(n)
nth term of geometric sequence = a(n) =

Where,
a = first term
r = common ratio
n = number of term
So,
GP: 3/4, 1, 4/3, 16/9
a = 3/4
r = 1 / [3/4] = 4/3
n = n
nth term of geometric sequence = a(n) =

nth term of geometric sequence = a(n) =