Question

If –3 + i is a root of the polynomial function f(x), which of the following must also be a root of f(x)?

Answer 1

If -3 + i is a root then -3 - i is too.

Therefore, the answer is -3 - i

Answer 2

Explanation:

REcall that f(x) is a polynomial whose one of its roots is -3+i. The fundamental algebra theorem states that any polynomial of degree n has n complex roots. In the real case, it can be also interpreted as any polynomial can be factored in factors of degree at most 2.

Consider that given a polynomial of degree 2 of the form
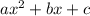`ax^2+bx+c` the solutions are given by

`x = \frac{-b \pm \sqrt[]{b^2-4ac}}{2a}`

In this case, the fact that x is real or complex depends on the number
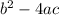`b^2-4ac` which is called the discriminant. When this number is negative, we have that x is a complex root. Let say that
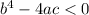`b^4-4ac<0` and that
`\sqrt[]{b^4-4ac}=di`, so the roots are given by

`x_1 = (-b + di)/(2a), x_2 = x_1 = (-b - di)/(2a)`

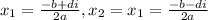
this means that, whenever we have a complex root, the other root is the complex conjugate. Recall that the complex conjugate of a complex number of the form a+bi is obtained by changing the sign of the imaginary part, that is a-bi.

So, in our case since -3+i is a root, then -3-i necessarily is another root.