Question

Represent the system of linear equations 3x+y-5=0 and 2x-y-5=0 graphically. From the graph write solution of the system and also the area of the triangle formed by the lines and y axis

Answer 1

The solution is (2, -1)

The area of the triangle formed is 10 square units.

Explanation:

The given system is

`3x+y-5=0\\2x-y-5=0`

First, you need to graph both lines. To do so, you just need to find the interceptions with both axis.

`3x+y-5=0`

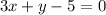
For
`x=0 \implies y=5`

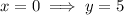
For
`y=0 \implies x=(5)/(3)`

Then, you draw both points to have the straight line.

Repeat the process for the second line. The image attached shows both lines.

Remember, the solution of a linear system of equation is the common point between lines. In this case, we can observe that the solution is (2, -1).

On the other hand, to find the area of the triangle formed, we need to use the length of its base and its height.

• Its base is 10 units long.
• Its height is 2 units long.

Now, we use the area formula for triangles

`A=(bh)/(2)=(10(2))/(2)= 10 \ u^(2)`

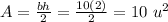
Therefore, the area of the triangle formed is 10 square units.