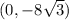Question

find the value of x and y if the distance of the point (x,y) from (-2,0) and (2,0) are both 14 units.​

Answer 1

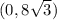`(0, 8√(3))` and
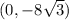`(0, -8√(3))` are both 14 units from points (-2, 0) and (2, 0).

Explanation:

distance formula

`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

We want the distance, d, from points (-2, 0) and (2, 0) to be 14.

Point (-2, 0):

`14 = √((x - (-2))^2 + (y - 0)^2)`

`√((x + 2)^2 + y^2) = 14`

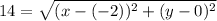
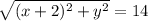
Point (2, 0):

`14 = √((x - 2)^2 + (y - 0)^2)`

`√((x - 2)^2 + y^2) = 14`

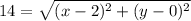
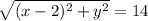
We have a system of equations:

`√((x + 2)^2 + y^2) = 14`

`√((x - 2)^2 + y^2) = 14`

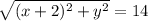
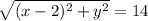
Since the right sides of both equations are equal, we set the left sides equal.

`√((x + 2)^2 + y^2) = √((x - 2)^2 + y^2)`

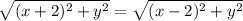
Square both sides:

`(x + 2)^2 + y^2 = (x - 2)^2 + y^2`

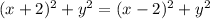
Square the binomials and combine like terms.

`x^2 + 4x + 4 + y^2 = x^2 - 4x + 4 + y^2`

`4x = -4x`

`8x = 0`

`x = 0`

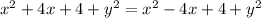
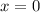
Now we substitute x = 0 in the first equation of the system of equations:

`√((x + 2)^2 + y^2) = 14`

`√((0 + 2)^2 + y^2) = 14`

`√(4 + y^2) = 14`

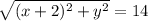
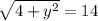
Square both sides.

`y^2 + 4 = 196`

`y^2 = 192`

`y = \pm √(192)`

`y = \pm √(64 * 3)`

`y = \pm 8√(3)`

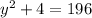
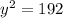
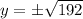
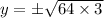
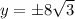
The points are:

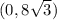`(0, 8√(3))` and
`(0, -8√(3))`