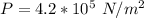Answer:
The gauge pressure is
Step-by-step explanation:
From the question we are told that
The height of the 14th floor from the point where the water entered the building is h = 43 m
The gauge pressure is mathematically represented as
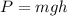
Where the m is the mass of the water which is mathematically represented as
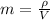
Where
 is the density of the water which has a constant value of
is the density of the water which has a constant value of
 and this standard value of density the volume is
and this standard value of density the volume is
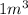 so
so

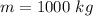
Thus