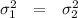Question

Suppose that E(θˆ1) = E(θˆ2) = θ, V(θˆ 1) = σ2 1 , and V(θˆ2) = σ2 2 . Consider the estimator θˆ 3 = aθˆ 1 + (1 − a)θˆ 2. a Show that θˆ 3 is an unbiased estimator for θ. b If θˆ1 and θˆ2 are independent, how should the constant a be chosen in order to minimize the variance of θˆ3?

Answer 1

Explanation:

Given that:

`E( \hat \theta _1) = \theta \ \ \ \ E( \hat \theta _2) = \theta \ \ \ \ V( \hat \theta _1) = \sigma_1^2 \ \ \ \ V(\hat \theta_2) = \sigma_2^2`

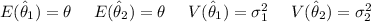
If we are to consider the estimator
`\hat \theta _3 = a \hat \theta_1 + (1-a) \hat \theta_2`

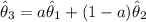
a. Then, for
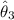`\hat \theta_3` to be an unbiased estimator ; Then:

`E ( \hat \theta_3) = E ( a \hat \theta_1+ (1-a) \hat \theta_2)`

`E ( \hat \theta_3) = aE ( \theta_1) + (1-a) E ( \hat \theta_2)`

`E ( \hat \theta_3) = a \theta + (1-a) \theta = \theta`

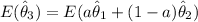
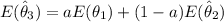
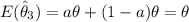
b) If
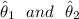`\hat \theta _1 \ \ and \ \ \hat \theta_2` are independent

`V(\hat \theta _3) = V (a \hat \theta_1+ (1-a) \hat \theta_2)`

`V(\hat \theta _3) = a ^2 V ( \hat \theta_1) + (1-a)^2 V ( \hat \theta_2)`

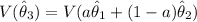
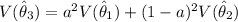
Thus; in order to minimize the variance of
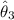`\hat \theta_3` ; then constant a can be determined as :

`V( \hat \theta_3) = a^2 \sigma_1^2 + (1-a)^2 \sigma^2_2`

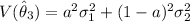
Using differentiation:

`(d)/(da)(V \ \hat \theta_3) = 0 \implies 2a \ \sigma_1^2 + 2(1-a)(-1) \sigma_2^2 = 0`

⇒

`a (\sigma_1^2 + \sigma_2^2) = \sigma^2_2`

`\hat a = (\sigma^2_2)/(\sigma^2_1+\sigma^2_2)`

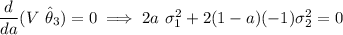
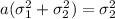
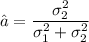
This implies that

`(d)/(da)(V \ \hat \theta_3)|_(a = \hat a) = 2 \ \sigma_1^2 + 2 \ \sigma_2^2 > 0`

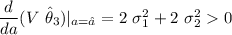
So,
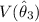`V( \hat \theta_3)` is minimum when
`\hat a = (\sigma_2^2)/(\sigma_1^2+\sigma_2^2)`

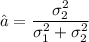
As such;
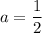`a = (1)/(2)` if
`\sigma_1^2 \ \ = \ \ \sigma_2^2`