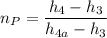Question

Water is the working fluid in an ideal Rankine cycle. Superheatedvapor enters the turbine at 10MPa, 480°C, and the condenser pressure is6 kPa. Isentropic efficiencies of the turbine and pump are 80% and 75%,respectively. Determine for the cyclea.the actual heat transfer to the working fluid passing through thesteam generator, in kJ per kg of steam flowing.b.the thermal efficiency.c.the actual heat transfer from the working fluid passing through thecondenser to the cooling water, in kJ per kg of steam flowing

Answer 1

Step-by-step explanation:

Given that:

Superheated vapor enters the turbine at 10 MPa, 480°C,

From the tables of superheated steam tables; the following values are obtained

`h_1 = 3322.02 \ kJ/kg\\\\ s_1 = 6.52846 \ kJ/kg.K`

Also; from the system, the isentropic line is 1-2 in which s_2 is in wet state

`s_2 = s_(f \ 6 kpa) +xs_(fg \ 6 kpa)`

`s_2 =0.51624 + x(7.82)`

`s_2 =0.51624 + 7.82x`

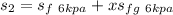
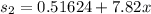
From the values obtained;

`s_1 =s_2= 6.52846 \ kJ/kg.K`

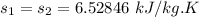
Therefore;

6.52846 = 0.51624+7.82x

6.52846 - 0.51624 = 7.82 x

6.01222 = 7.82 x

x = 6.01222/7.82

x = 0.7688

The enthalpy for this process at state (s_2) can be determined as follows:

`h_2 = h _f +xh_(fg) \\ \\ h_2 = 150.15 +(0.77 * 2415.92) \\ \\ h_2 =150.15 +( 1629.2584 ) \\ \\ h_2 =2010.4084 \ kJ/kg`

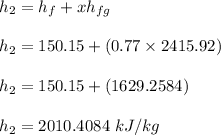
The actual enthalpy at s_2 by using the isentropic efficiency of the turbine can determined by using the expression:

`n_T = (h_1-h_(2a))/(h_1-h_2)`

`0.8 = (3322.02-h_(2a))/(3322.02-2010.4084)`

`0.8 = (3322.02-h_(2a))/(1311.6116)`

`0.8 * {1311.6116}= {3322.02-h_(2a)`

`1049.28928= {3322.02-h_(2a)`

`h_(2a)= {3322.02- 1049.28928`

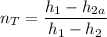
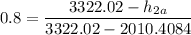
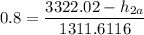
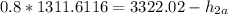
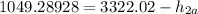
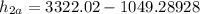
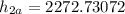`h_(2a)= 2272.73072` kJ/kg

The work pump is calculated by applying the formula:

`w_p = v_(f \ 6 kpa) (p_4-p_3)`

`w_p = 0.0010062 * (10000-6)`

`w_p = 0.0010062 *9994`

`w_p = 10.0559628 \ kJ/kg`

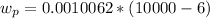
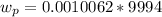
However;

`w_p = h_4 -h_3`

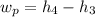
From the process;

`h_3 = h_(f(6 kpa)) = 150.15 \ kJ/kg`

`10.0559628 = h_4 - 150.15`

`10.0559628+ 150.15 = h_4`

`160.2059628= h_4`

`h_4= 160.2059628 \ kJ/kg`

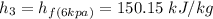
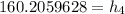
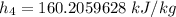
The actual enthalpy at s_4 by using the isentropic efficiency of the turbine can determined by using the expression:

`n_P = (h_4-h_(3))/(h_(4a)-h_3)`