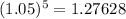The question is incomplete! Complete question along with answer and step by step explanation is provided below.
Question:
Use the generalized binomial expansion to expand (1 + x)^a up to the a = 5 and hence determine (1.05)^5. to 5 decimal places.
Answer:
Using the binomial theorem
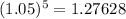
Explanation:
The binomial theorem is given by
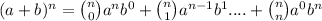
For the given case, we have
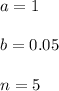
So,
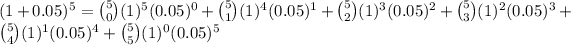
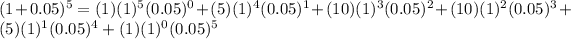
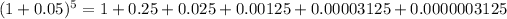
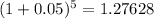
Therefore, using the binomial theorem