Question

If you were to experimentally determine the length of the pendulum, why would you not get the same length in Iowa?

Answer 1

The length of the pendulum depends on acceleration due to gravity (g) which varies in different Earth's location beacuse Earth is not perfectly spherical.

Step-by-step explanation:

The period of oscillation is calculated as;

`T = 2\pi\sqrt{(l)/(g) }`

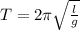
where;

L is the length of the pendulum bob

g is acceleration due to gravity

If we make L the subject of the formula in the equation above, we will have;

`T = 2\pi\sqrt{(l)/(g)}\\\\\sqrt{(l)/(g) } = (T)/(2\pi) \\\\(l)/(g) = ((T)/(2\pi) \)^2\\\\(l)/(g) =(T^2)/(4\pi^2)\\\\L = (gT^2)/(4\pi^2)`

The length of the pendulum depends on acceleration due to gravity (g).

Acceleration due to gravity is often assumed to be the same everywhere on Earth, but it varies because Earth is not perfectly spherical. The variation of acceleration due to gravity (g) as a result of Earth's geometry, will also cause the length of the pendulum to vary.