Question

Select all that apply. A direct variation equation is graphed. The point (6, 4) is on the graph. Which of the following points are also on the graph of the equation? (3, 2) (-9, -6) (-12, 8) (-6, -3)

Answer 1

(-9, -6) and (3, 2)

Explanation:

Answer 2

(3,2)

(-9,-6)

Explanation:

Given that the graph is a direct variation.

The equation of variation is:

`x=ky`

Since point (6, 4) is on the graph

`6=4k\\\\k=\frac64`

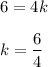
Therefore, the equation connecting x and y is:

`x=\frac64y`

`\text{When y=2},x=\frac64 * 2 =3\\\\\text{When y =}-6,x=\frac64 * -6 =-9\\\\\text{When y =}8,x=\frac64 * 8 =12\\\\\text{When y =}-3,x=\frac64 * -3 =-4.5`

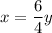
Therefore, the points that are also on the graph are:

(3,2) and (-9,-6)