Question

Which of the following is a point-slope equation of a line that passes through

the points (5,2) and (-1,-6)?
A. y-2-(X-5)
B. y-2-(X-5)
C. y-2 =(x-5
D. V-2--0-5)

Answer 1

Please, check the options of the question. The point-slope equation needs the slope, m, in the equation.

Answer:

The point-slope equation of the points (5,2) and (-1,-6) is

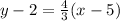`\\ y - 2 = (4)/(3)(x-5)` or,

`\\ y + 6 = (4)/(3)(x+1)`

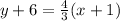
which are the same as

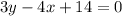`\\ 3y-4x+14 = 0` , (which is not a point-slope equation, though)

Explanation:

The point-slope equation is given by:

`\\ y - y_(1) = m(x - x_(1))`

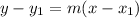
Where m is the slope of the line:

`\\ m = (y_(2) - y_(1))/(x_(2) - x_(1))`

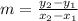
Having the points (5,2) and (-1,-6), then

`\\ m = (-6 - 2)/(-1 -5)`

`\\ m = (-8)/(-6)`

`\\ m = (4)/(3)`

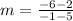
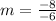
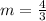
Then, the point-slope equation of the points (5,2) and (-1,-6) is

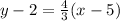`\\ y - 2 = (4)/(3)(x-5)` or

`\\ y + 6 = (4)/(3)(x+1)`

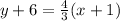
The below graph represents both lines (they are the same line).